短路与短路比

作者：邹德虎

2024-08-05整理

返回主页

本文不是对于短路电流计算、短路比等理论进行全面论述，而是从简单模型出发的小思考，希望能够加深对某些概念的理解。

1 短路电流的本质

首先是短路电流算法的本质，我认为是电力系统结构变化情况下，用最简化的方式计算短期电磁暂态的关键物理量。这里的结构变化，包括接地短路、断线，还包括断路器合环（包括输电网的断路器合闸、配电网的馈线合环），还包括AVC中电容器的投切。这些结构变化问题都可以用基本相同的数学模型来分析，只不过具体的结构变化不同、边界条件不同而已。当然，按照我的定义，叫短路电流计算不合适，叫故障分析也不合适。但为了约定俗成，本文名词术语就不更改了。

下面我们再来看看，我们常说的“短路电流”，到底是什么？我们可以建立最简单模型：就是包含内部电阻和电抗的戴维南等值电压源，进行合闸。

对于该模型，如果两个节点，有一个是接地点，另一个是正常节点，可以表示接地故障。如果两个节点都是正常的电力系统节点，中间是忽略了阻抗的断路器，那么可以表示断路器合环。不管怎么样，通过假设最不利的合闸条件和进行简单的数学计算，可以得到下面的曲线图：

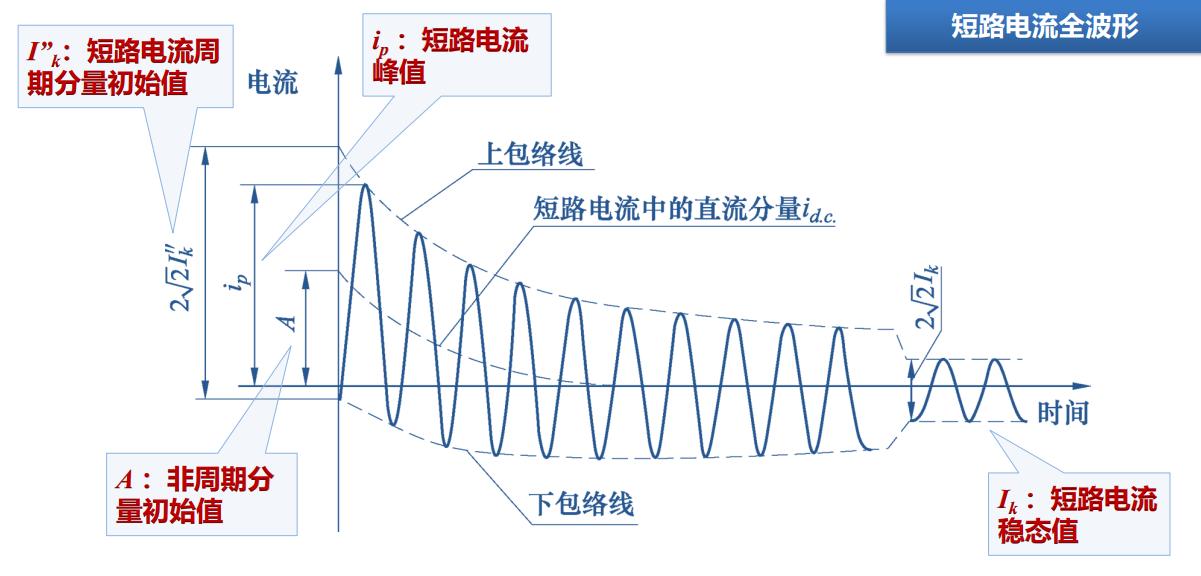
（该图拷贝自中国电科院王虹富的培训PPT，在此表示感谢）

我们通常说的短路电流指的是周期分量初始值(有效值)。对于保护装置，可以很容易通过快速傅里叶算法分离出该分量。同样的电力系统，发生故障就是这个数值，这样预先设定的保护整定值就可以发挥作用。其它的物理量就不行，比如说冲击电流，可大可小，跟具体合闸角度有关。我们如果把实际故障的录波曲线和电磁暂态仿真曲线做对比，是很难完全一致的，不可控因素太多了。

这个短路电流周期分量是会衰减的，具体衰减到什么程度呢？可以对结构变化后的电力系统再做一次潮流计算（不要以为带故障的电力系统就不能算潮流了）。但大家不太关心短路电流分量稳态值。因为现代保护的动作速度是非常快的，在几个周波之内（就算加上断路器灭弧时间）就可切除故障，这时候周期分量衰减很小，基本上相当于短路电流周期分量初值，也就是我们说的短路电流值。

关于短路电流计算究竟对电力系统模型进行了哪些简化？一般的教科书都会有详细论述，包括认为d轴次暂态电抗和q轴次暂态电抗相等、忽略定子回路电磁过程，等等。还有一点我觉得可以强调：短路电流忽略了所有控制过程（最典型的就是忽略了发电机励磁控制），一方面因为保护装置所需要观察的时间短，控制的影响不太大；另一方面，短路电流计算把复杂的电磁暂态仿真变成简单的代数计算，势必忽略所有的控制，因为控制总是涉及传递函数、微分方程的求解。

这也能解释，为什么短路电流计算不可以直接用潮流计算的导纳矩阵，而是要对潮流计算导纳矩阵进行一些处理，具体的处理包括：1）发电机节点对角元加上接地的次暂态电抗；2）PQ节点功率转换为等值阻抗，加入对角元；3）必要时考虑感应电动机可能会提供短路电流。

因为潮流计算模型假定包含了控制的结果，比如，世界上不存在PV节点，所谓PV节点是发电机励磁控制后的效果。PQ节点也是如此，隐含了定功率控制的假设。短路电流计算忽略控制；潮流计算模型包含控制，而且时间尺度不适合只有几个周波的暂态过程。因此短路电流计算不能直接用潮流的导纳矩阵，必须把PQ节点加上等值的阻抗，这样减少了误差。至于对角元加上接地的次暂态电抗，其实是对发电机提供短路电流的一种刻画。

下面再谈一谈断路器合环电流的计算，具体计算的核心步骤其实就是潮流计算结果加上戴维南等值。

有的公司合环潮流的产品，直接使用潮流计算的导纳矩阵，这是不妥的。但是可以注意到：1）合环潮流主要应用到地区电网，地调管辖范围内一般不会有大型发电机；2）地区电网一般有500kV变电站，最好的处理方式是在500kV电网挂载一个等值发电机，其等值电抗由当地的短路容量换算出来。在这两种因素的影响下，合环潮流的计算误差不一定很大。

顺便说一句，有的厂家合环潮流计算的产品走入了另一个误区，采用复杂的电磁暂态仿真给出结果。实际上，合环校验主要看电流周期分量是否会引起保护误动作，其次再查看冲击电流。因此，合环校验的精度要求跟普通的短路电流计算是一致的。地市级供电公司是生产单位，很难组成技术团队把电网暂态仿真模型维护好，这个维护成本是相当高的。

下面再谈谈一个有趣的例子，是关于电容器投切的计算，有些人可能觉得这个跟短路电流风马牛不相及，其实不是。如下图所示，地区电网变电站，投入电容器，已知电容器容量，希望计算出电压的变化。

这个问题可以用潮流计算的灵敏度来分析，但是工业现场的灵敏度计算，未必和教科书里面的一样简单，里面是有“坑”存在的。但是借助短路容量的概念很容易推导，推导如下。

首先假设母线短路容量是$S_d$，额定电压是$V_N$.我们投入电容器，容量是$Q$，我们假设母线到等值发电机的电抗为$X$，等值发电机的内部电抗我们暂时忽略掉，因为相比地区电网配电网，输电网的等值发电机内部电抗是相当小的。下面我们想求出电压变化量$\delta V$。

根据叠加原理，可以得到(请注意这个式子并不是非常严格的)：

$$\frac{Q}{S_d} \approx \frac{\delta V}{V_N}$$

进一步的，可以得到：

$$Q = S_d\frac{\delta V}{V_N} \\ = \frac{V_N^2}{X} \frac{\delta V}{V_N} \\ = \frac{V_N}{X} \delta V$$

从而可以很容易估计出电压变化量。

可能会有人疑问，电容器无功容量可以直接除以短路容量吗，单位是否相同？事实上，我们假设了电网电抗远大于电阻，忽略电阻。那么这种情况下短路容量是无功，短路电流是无功电流。这一点可以由反证法论证：对于单机无穷大系统暂态稳定分析的等面积法则，出现了故障，降低输送能力，此时电磁功率会下降。如果短路容量是有功，而且很可能这个数值超过发电机初始有功输送功率，那就不符合能量守恒了。

这里要注意，我们关心的电容器投入产生的电流，一定是电流周期分量稳态值而不是电流周期初始值，这时候如果使用导纳阵，应该用潮流计算的导纳阵。好在我们引入短路容量，并建立等值发电机，本身就是近似模型，这个计算也属于工程实用算法。

2 短路比的讨论

随着新型电力系统电力电子化的趋势加快，直流和新能源的短路比的概念越来越得到讨论和重视。其实，短路比不限于电力电子变流器的接入，传统的同步电机并网稳定性也可以用短路比来刻画。下面是短路比概念的有关简化公式推导，希望有一点点启发意义。

如下图所示，考虑最简单的并网模型：

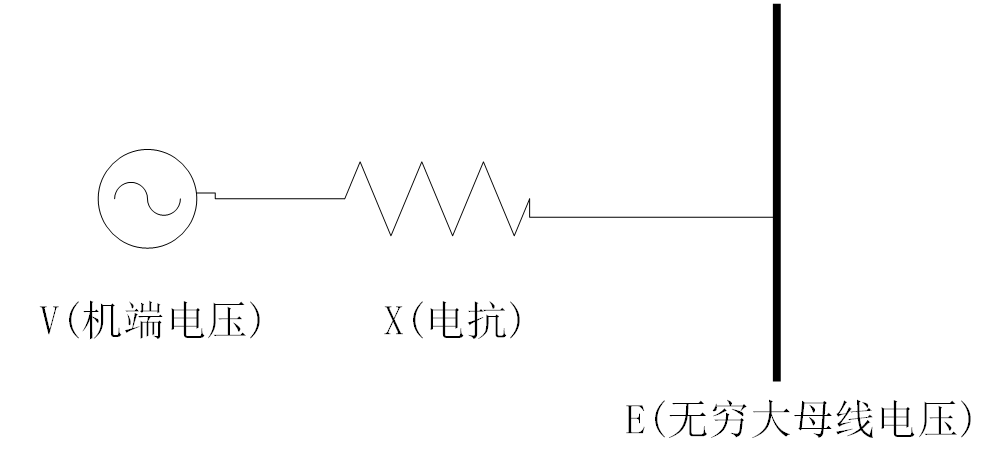
我们考虑单机无穷大系统。这里的单机电源可以是同步电机，也可以是新能源。则机端的有功P、无功Q和短路容量S可表示为：

$$P = \frac{E V}{X} \sin \delta$$

$$Q = \frac{V^2-EV\cos\delta}{X}$$

$$S =\frac{E^2}{X}$$

我们定义定义短路比为：

$$K =\frac{S}{P}$$

下面考虑两种情况：

情况1 电源具有极强的电压控制能力，例如采取现代自并励控制的同步电机。可以维持机端电压幅值V几乎不变，则可以求出最大输送有功功率：

$$P_{MAX} =\frac{EV}{X} \approx \frac{E^2}{X} = S$$

那么，同步电机的静态功角的稳定判据可以用短路比表达，为：

$$K>1$$

当然，这里是忽略了静态稳定储备系数。

情况2 电源完全没有电压控制能力，但是存在锁相环，具有相位跟随能力。我们假设只发出有功功率，此时可以简化成负电阻的负荷。此时存在：

$$P^2 = \frac{E^2 V^2}{X^2} \sin^2 \delta = \frac{E^2 V^2}{X^2} (1-\cos^2 \delta)$$

$$Q = \frac{V^2-EV\cos\delta}{X} =0$$

可以推导出：

$$P^2 = \frac{E^2 V^2}{X^2} -\frac{V^4}{X^2}$$

求出最大有功功率，可以先求导。再令导数为0，求出V，最后得到：

$$P_{MAX} =\frac{1}{2}\frac{E^2}{X} = \frac{1}{2}S$$

如果改成短路比的表达式，则为：

$$K>2$$

进一步讨论

对于变流器的控制来说，外环控制完全不考虑电压是不太可能的。事实上，构网型电力电子控制，就是希望模拟出电压源（甚至模拟出虚拟的频率、惯量/阻尼/下垂控制）。但构网型模拟的再好，也比不过同步发电机自身。（另外要考虑到大量跟网型变流器的存在）。因此，新能源的短路比不等式，应当介于1和2之间。目前业界普遍认为：实际现场的新能源短路比，最低程度是1.5，再低就几乎必然不稳定了。正好是本文1和2的平均数。

实际上，静态稳定都是有裕度的。按照《电力系统安全稳定导则》，静态稳定储备系数应满足10%~15%，换算后，对于同步电机来说是相当于短路比大于1.85左右。如果对于新能源来说，短路比应该放的更大一些才好。这一点与规范是一致的。《电力系统安全稳定计算规范》规定：“新能源并网点的多场站短路比应不小于2.0，宜大于3.0”。

按照本文的推导，可以认为短路比是电力系统静态稳定的另外一种表述（而且揉合了功角稳定和电压稳定），而且具有更好的工程实用性。